An interesting question was raised by a user about the placement of the vertical symmetry planes for C4v molecules in the Gallery. If we look at the BrF5 example specifically, the question becomes:
should the vertical (σv) planes each pass through four atoms (the bromine atom and three of the fluorine atoms) with the dihedral (σd) planes in between or vice versa?
Two possible orientations of the BrF5 molecule, relative to the x and y axes, are shown in Figure 1. (By convention, the 4-fold axis is aligned with the z axis.)
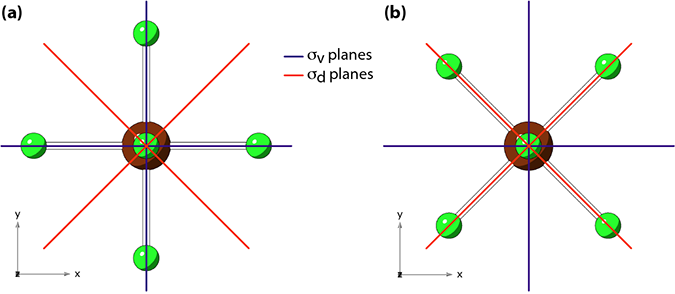
Figure 1: Two possible orientations of the BrF5 molecule
Information from the character table: The placement of the σv and σd planes (relative to the coordinate axes) is determined by the character table. As shown below, the xy function (think dxy orbital), undergoes a change in sign with σv and no change in sign with σd. Therefore the σv planes must be coincident with the xz and yz planes.
| C4v | E | 2 C4 | C2 | 2 σv | 2 σd | quadratic |
|---|---|---|---|---|---|---|
| A1 | 1 | 1 | 1 | 1 | 1 | x2 + y2, z2 |
| A2 | 1 | 1 | 1 | -1 | -1 | |
| B1 | 1 | -1 | 1 | 1 | -1 | x2 + y2 |
| B2 | 1 | -1 | 1 | -1 | 1 | xy |
| E | 2 | 0 | -2 | 0 | 0 | (xz, yz) |
Nomenclature: For the C4v point group, the second set of vertical symmetry planes should technically not even be called σd – a label of σv' would be more appropriate.1 The C4v point group does not contain any C2 axes perpendicular to the principle axis, and the σd label is typically given to planes that contain the principle axes and pass between sets of perpendicular C2 axes. But the σd label is very commonly used for the C4v character tables and is used in the Symmetry Gallery.
Choosing an orientation: But neither of these help decide between choices (a) and (b) in Figure 1. There seems to be a loosely defined convention that σv planes bisect as many atoms as possible.2 This would give preference to choice (a). But is is important to note that this selection is actually arbitrary3 and may not be followed by others.
An example: The vibrational analysis of [Mn(CO)5Br] serves as a good example. Using orientations analogous to Figures 1a and 1b, we can generate the following reducible representations for the CO stretching vibrations in [Mn(CO)5Br]:
| C4v | E | 2 C4 | C2 | 2 σv | 2 σd |
|---|---|---|---|---|---|
| ΓCO (Fig 1a) | 5 | 1 | 1 | 3 | 1 |
| ΓCO (Fig 1b) | 5 | 1 | 1 | 1 | 3 |
Reduction of the first representation (Fig 1a) gives a set of CO stretching vibrations corresponding to 2 A1 + B1 + E1, consistent with published normal coordinate analyses.4 Vibrational analysis using Spartan 18 or WebMO (MOPAC), however, will give a set of vibrations as 2 A1 + B2 + E1, consistent with the second representation (1b). It is not completely clear (to me) why this is the case, but I would note that some symmetry optimization algorithms (e.g. SYMMOL) will select the orientation shown in Figure 1b by default.
Conclusion: The orientation of the symmetry planes in C4v (or 4mm), regardless of how they are labeled, is determined by the character table. Therefore the σv planes will be coplanar with the xz and yz planes and the σd (or σv') planes pass in between. The orientation of the molecule, other than aligning the Cv axis with the z axis, is arbitrary. Many prefer to align the bonds to correspond with the σv planes, but it is not required.
-
In Symmetry and Structure: Readable Group Theory for Chemists, Sidney Kettle notes that the σd label should only be applied to symmetry planes that pass between two C2 axes. ↩︎
-
See CHEM 2060 Lecture Notes from the University of Guelph or other online discussions. ↩︎
-
Kettle notes that there are actually an infinite number of possible orientations of BrF5 (all acceptable and workable), but the two given in Figure 1 make calculations easier. ↩︎
-
See Cotton, F. A.; Musco, A.; Yagupsky, G., Inorg. Chem. 1967, 6(7), 1357–1364 (DOI); Kaesz, H. D.; Bau, Robert.; Hendrickson, David.; Smith, J. Michael., J. Am. Chem. Soc. 1967, 89(12), 2844–2851 (DOI); Hyam, I. J.; Lippincott, E. R., Spectrochim. Acta A 1969, 25(12), 1845–1854 (DOI). ↩︎